Predicting profit generated by movies
Python
In my last post, I tested several models that predicted movie ratings. This time, I’ll try and predict the gross profit a movie might generate based on the same features. The aim is to create a Flask app that will allow a user to see the predicted rating and gross profit for a movie they create based on certain feature choices (ie. cast, director, genre).
Since all the data cleaning was done in my last blog post, I can move straight into the exploratory data analysis.
Set up and import data
import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
import seaborn as sns
import pickle
from sklearn import linear_model as lm, metrics, tree, ensemble, svm
from sklearn.model_selection import train_test_split, KFold, cross_val_score, GridSearchCV
from sklearn.preprocessing import StandardScaler
%matplotlib inline
pd.options.mode.chained_assignment = None
pd.set_option('display.max_columns', 500)
pd.set_option('display.max_rows', 5000)
np.random.seed(42)
sns.set(rc={
'figure.figsize': (12, 8),
'font.size': 14
})
# Set palette
sns.set_palette("husl")
movies = pd.read_csv("/Users/jasminepengelly/Desktop/projects/predicting_movie/movies_wo_dir.csv")
movies.drop("Unnamed: 0", axis=1, inplace=True)
movies["gross_profit"] = movies["revenue"] - movies["budget"]
movies.head()
| title | id | budget | revenue | runtime | vote_average | vote_count | belongs_to_collection | Action | Adventure | Animation | Aniplex | BROSTA TV | Carousel Productions | Comedy | Crime | Documentary | Drama | Family | Fantasy | Foreign | GoHands | History | Horror | Mardock Scramble Production Committee | Music | Mystery | Odyssey Media | Pulser Productions | Rogue State | Romance | Science Fiction | Sentai Filmworks | TV Movie | Telescene Film Group Productions | The Cartel | Thriller | Vision View Entertainment | War | Western | lead | supporting | dir_count | gross_profit | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | Toy Story | 862 | 30000000.0 | 373554033.0 | 81.0 | 7.7 | 5415.0 | 1 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | Tom Hanks | Tim Allen | 5 | 343554033.0 |
| 1 | Jumanji | 8844 | 65000000.0 | 262797249.0 | 104.0 | 6.9 | 2413.0 | 0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | Robin Williams | Jonathan Hyde | 7 | 197797249.0 |
| 2 | Heat | 949 | 60000000.0 | 187436818.0 | 170.0 | 7.7 | 1886.0 | 0 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 | Al Pacino | Robert De Niro | 10 | 127436818.0 |
| 3 | Sudden Death | 9091 | 35000000.0 | 64350171.0 | 106.0 | 5.5 | 174.0 | 0 | 1.0 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 | Jean-Claude Van Damme | Powers Boothe | 10 | 29350171.0 |
| 4 | GoldenEye | 710 | 58000000.0 | 352194034.0 | 130.0 | 6.6 | 1194.0 | 1 | 1.0 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 | Pierce Brosnan | Sean Bean | 8 | 294194034.0 |
Exploratory data analysis
From my previous analysis, I know there is a relatively high correlation between budget, revenue and vote_count. This time around I’ll focus on the relationships between revenue and the other variables.
First, I’ll define the variables that I’m using.
X = ['budget', 'runtime', 'vote_count', 'belongs_to_collection', 'Action', 'Adventure',
'Animation', 'Aniplex', 'BROSTA TV', 'Carousel Productions', 'Comedy', 'Crime', 'Documentary', 'Drama',
'Family', 'Fantasy', 'Foreign', 'GoHands', 'History', 'Horror', 'Mardock Scramble Production Committee',
'Music', 'Mystery', 'Odyssey Media', 'Pulser Productions', 'Rogue State', 'Romance', 'Science Fiction',
'Sentai Filmworks', 'TV Movie', 'Telescene Film Group Productions', 'The Cartel', 'Thriller',
'Vision View Entertainment', 'War', 'Western', 'lead', 'supporting', 'vote_average']
y = 'gross_profit'
sns.heatmap(movies.drop(['title', 'id', 'dir_count'], axis=1).corr(), vmin=-1, vmax=1, center=0, cmap=sns.diverging_palette(10, 220, sep=80, n=7))
<matplotlib.axes._subplots.AxesSubplot at 0x1a1aabd240>
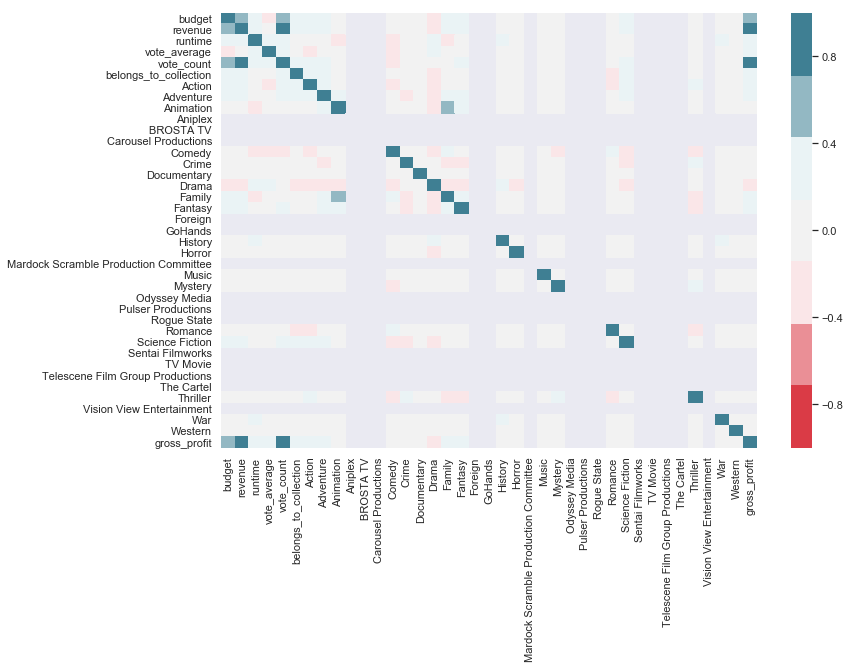
My response variable, gross_profit, is highly correlated with budget, revenue and vote_ count. budget and revenue make sense, since the three are directly related, but vote_ count is less intuitive - perhaps more votes are to be expected on popular films, and films with a high budget or that make large revenue get more votes.
Within my features, I already identified the correlation between Family and Animation, and vote_count and budget, are not significant enough to worry about. This bodes well for my models - there will be no multicollinearity and there is no need for PCA here.
Highest revenue films
high_rev = movies[['title', 'revenue']].sort_values(by = 'revenue', ascending = False).head(10)
high_rev['revenue'] = high_rev['revenue'].map('${:,.2f}'.format)
high_rev
| title | revenue | |
|---|---|---|
| 1439 | Avatar | $2,787,965,087.00 |
| 1766 | Star Wars: The Force Awakens | $2,068,223,624.00 |
| 328 | Titanic | $1,845,034,188.00 |
| 1778 | Furious 7 | $1,506,249,360.00 |
| 1540 | Harry Potter and the Deathly Hallows: Part 2 | $1,342,000,000.00 |
| 1875 | Beauty and the Beast | $1,262,886,337.00 |
| 1881 | The Fate of the Furious | $1,238,764,765.00 |
| 1535 | Transformers: Dark of the Moon | $1,123,746,996.00 |
| 994 | The Lord of the Rings: The Return of the King | $1,118,888,979.00 |
| 1614 | Skyfall | $1,108,561,013.00 |
Highest grossing films
high_gp = movies[['title', "gross_profit"]].sort_values(by = "gross_profit", ascending = False).head(10)
high_gp["gross_profit"] = high_gp["gross_profit"].map('${:,.2f}'.format)
high_gp
| title | gross_profit | |
|---|---|---|
| 1439 | Avatar | $2,550,965,087.00 |
| 1766 | Star Wars: The Force Awakens | $1,823,223,624.00 |
| 328 | Titanic | $1,645,034,188.00 |
| 1778 | Furious 7 | $1,316,249,360.00 |
| 1540 | Harry Potter and the Deathly Hallows: Part 2 | $1,217,000,000.00 |
| 1875 | Beauty and the Beast | $1,102,886,337.00 |
| 994 | The Lord of the Rings: The Return of the King | $1,024,888,979.00 |
| 1881 | The Fate of the Furious | $988,764,765.00 |
| 1535 | Transformers: Dark of the Moon | $928,746,996.00 |
| 1614 | Skyfall | $908,561,013.00 |
Lowest revenue films
low_rev = movies[['title', 'revenue']].sort_values(by = 'revenue', ascending = True).head(10)
low_rev['revenue'] = low_rev['revenue'].map('${:,.2f}'.format)
low_rev
| title | revenue | |
|---|---|---|
| 576 | Angela's Ashes | $13.00 |
| 1271 | Death at a Funeral | $46.00 |
| 628 | The Idiots | $7,235.00 |
| 1604 | 5 Days of War | $17,479.00 |
| 590 | City Lights | $19,181.00 |
| 1464 | Valhalla Rising | $30,638.00 |
| 480 | Following | $48,482.00 |
| 1678 | The Canyons | $56,825.00 |
| 1628 | Byzantium | $89,237.00 |
| 1796 | Manglehorn | $143,101.00 |
Biggest loss
high_gp = movies[['title', "gross_profit"]].sort_values(by = "gross_profit", ascending = True).head(10)
high_gp["gross_profit"] = high_gp["gross_profit"].map('${:,.2f}'.format)
high_gp
| title | gross_profit | |
|---|---|---|
| 1673 | The Lone Ranger | $-165,710,090.00 |
| 1011 | The Alamo | $-119,180,039.00 |
| 1884 | Valerian and the City of a Thousand Planets | $-107,447,384.00 |
| 513 | The 13th Warrior | $-98,301,101.00 |
| 7 | Cutthroat Island | $-87,982,678.00 |
| 1365 | Australia | $-80,445,998.00 |
| 578 | Supernova | $-75,171,919.00 |
| 1080 | A Sound of Thunder | $-74,010,360.00 |
| 1128 | The Great Raid | $-69,833,498.00 |
| 1674 | R.I.P.D. | $-68,351,500.00 |
Import directors and get dummy variables
directors = pd.read_csv("/Users/jasminepengelly/Desktop/projects/predicting_movie/director_dummies.csv")
directors.drop("Unnamed: 0", axis=1, inplace=True)
final = pd.merge(directors, movies, left_on = 'index', right_on = 'id')
final.drop(["id", "index", "title", "dir_count"], axis=1, inplace=True)
dummies = pd.get_dummies(final, columns=['lead', 'supporting'], drop_first=True)
Pre-processing
Since the final product of this modelling is to produce a Flask app that allows someone to input factors about a film before it’s produced to get the rating and the gross profit generated, some features will have to be dropped. For example, a user would not know the vote_count before the film is created. Some of the features I am removing are the most correlated with the response variable so I will be losing some of the predictive power.
I’ll begin by defining my train-test split. Then, as with my previous blog post, I’ll standardise the remaining predictive variables since it’s good practice for working with linear regression models.
X = dummies.drop(["revenue", "vote_count", "gross_profit", "vote_average"], axis=1)
y = dummies["gross_profit"]
scaler = StandardScaler()
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
X_train = pd.DataFrame(scaler.fit_transform(X_train), columns=X.columns)
X_test = pd.DataFrame(scaler.transform(X_test), columns=X.columns)
print("Length of training sets:",len(X_train), len(X_test))
print("Length of testing sets:",len(y_train), len(y_test))
Length of training sets: 1320 567
Length of testing sets: 1320 567
Modelling
Baseline score
I need a baseline score with which to compare the scores for all my models moving forward. This score will represent the score one would get if they were just to predict the mean value for y. If my model outperforms this score, I know it is doing well.
y_pred_mean = [y_train.mean()] * len(y_test)
print("Dumb model RMSE: ",'${:,.2f}'.format(np.sqrt(metrics.mean_squared_error(y_test, y_pred_mean))))
Dumb model RMSE: $226,516,599.51
$226 million will be the benchmark RMSE for my model’s success. It’s still a very wide margin to be out by, so I’m hoping I can beat this.
Function to generate model scores
Since I’ll be trying out many different models, I’ll build a function that returns all the information for efficiency. I’ll create one function for simple models and another for models utilising regularisation.
If this were a function I was using regularly, I would put it in a script and import it. However, I wanted it explicitly stated here for you to see.
# Function to return simple model metrics
def get_model_metrics(X_train, y_train, X_test, y_test, model, parametric=True):
"""This function takes the train-test splits as arguments, as well as the algorithm
being used, and returns the training score, the test score (both RMSE), the
cross-validated scores and the mean cross-validated score. It also returns the appropriate
feature importances depending on whether the optional argument 'parametric' is equal to
True or False."""
model.fit(X_train, y_train)
train_pred = np.around(model.predict(X_train),1)
test_pred = np.around(model.predict(X_test),1)
print('Training RMSE:', '${:,.2f}'.format(np.sqrt(metrics.mean_squared_error(y_train, train_pred))))
print('Testing RMSE:', '${:,.2f}'.format(np.sqrt(metrics.mean_squared_error(y_test, test_pred))))
cv_scores = -cross_val_score(model, X_train, y_train, cv=5, scoring='neg_mean_squared_error')
print('Cross-validated RMSEs:', np.sqrt(cv_scores))
print('Mean cross-validated RMSE:', '${:,.2f}'.format(np.sqrt(np.mean(cv_scores))))
if parametric == True:
print(pd.DataFrame(list(zip(X_train.columns, model.coef_, abs(model.coef_))),
columns=['Feature', 'Coef', 'Abs Coef']).sort_values('Abs Coef', ascending=False).head(10))
else:
print(pd.DataFrame(list(zip(X_train.columns, model.feature_importances_)),
columns=['Feature', 'Importance']).sort_values('Importance', ascending=False).head(10))
return model
# Function to return regularised model metrics
def regularised_model_metrics(X_train, y_train, X_test, y_test, model, grid_params, parametric=True):
"""This function takes the train-test splits as arguments, as well as the algorithm being
used and the parameters, and returns the best cross-validated training score, the test
score, the best performing model and it's parameters, and the feature importances."""
gridsearch = GridSearchCV(model,
grid_params,
n_jobs=-1, cv=5, verbose=1, error_score='neg_mean_squared_error')
gridsearch.fit(X_train, y_train)
print('Best parameters:', gridsearch.best_params_)
print('Cross-validated score on test data:', '${:,.2f}'.format(abs(gridsearch.best_score_)))
best_model = gridsearch.best_estimator_
print('Testing RMSE:', '${:,.2f}'.format(np.sqrt(metrics.mean_squared_error(y_test, best_model.predict(X_test)))))
if parametric == True:
print(pd.DataFrame(list(zip(X_train.columns, best_model.coef_, abs(best_model.coef_))),
columns=['Feature', 'Coef', 'Abs Coef']).sort_values('Abs Coef', ascending=False).head(10))
else:
print(pd.DataFrame(list(zip(X_train.columns, best_model.feature_importances_)),
columns=['Feature', 'Importance']).sort_values('Importance', ascending=False).head(10))
return best_model
Linear regression
Simple
lr = get_model_metrics(X_train, y_train, X_test, y_test, lm.LinearRegression())
lr
Training RMSE: $43,093,674.65
Testing RMSE: $6,850,145,181,265,346,691,072.00
Cross-validated RMSEs: [4.17892339e+21 9.90531764e+21 1.53491007e+22 1.13727100e+22
5.58558345e+21]
Mean cross-validated RMSE: $10,116,431,047,916,374,720,512.00
Feature Coef Abs Coef
1088 supporting_Bijou Phillips 1.347614e+21 1.347614e+21
276 Telescene Film Group Productions -1.259300e+21 1.259300e+21
266 Mardock Scramble Production Committee 1.202241e+21 1.202241e+21
665 lead_Judi Dench -1.150649e+21 1.150649e+21
1951 supporting_Seth Green -1.078695e+21 1.078695e+21
584 lead_James Woods -1.075888e+21 1.075888e+21
428 lead_Cuba Gooding Jr. 1.031542e+21 1.031542e+21
25 Bill Condon 1.029315e+21 1.029315e+21
1212 supporting_Dan Stevens -1.012743e+21 1.012743e+21
1011 supporting_Adrienne Barbeau -9.823532e+20 9.823532e+20
LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)
Both my scores are terrible here, and the vast difference between the scores show the level of overfitting. Time for some regularisation.
Regularised - Ridge
ridge = lm.Ridge()
ridge_params = {'alpha': np.linspace(600, 800, 5),
'fit_intercept': [True, False],
'solver': ['auto', 'svd', 'cholesky', 'lsqr', 'sparse_cg', 'sag', 'saga']}
ridge_model = regularised_model_metrics(X_train, y_train, X_test, y_test, ridge, ridge_params)
Fitting 5 folds for each of 70 candidates, totalling 350 fits
[Parallel(n_jobs=-1)]: Done 42 tasks | elapsed: 9.3s
[Parallel(n_jobs=-1)]: Done 192 tasks | elapsed: 35.6s
[Parallel(n_jobs=-1)]: Done 350 out of 350 | elapsed: 1.1min finished
Best parameters: {'alpha': 700.0, 'fit_intercept': True, 'solver': 'saga'}
Cross-validated score on test data: $0.36
Testing RMSE: $185,680,100.81
Feature Coef Abs Coef
249 belongs_to_collection 2.131550e+07 2.131550e+07
247 budget 2.086358e+07 2.086358e+07
82 George Lucas 1.426045e+07 1.426045e+07
248 runtime 1.330278e+07 1.330278e+07
437 lead_Daniel Radcliffe 1.128897e+07 1.128897e+07
1918 supporting_Rupert Grint 1.100804e+07 1.100804e+07
1976 supporting_Stanley Tucci 9.935829e+06 9.935829e+06
1395 supporting_Ian McKellen 9.889183e+06 9.889183e+06
251 Adventure 9.849955e+06 9.849955e+06
491 lead_Emma Watson 9.219124e+06 9.219124e+06
This test score is already better than the baseline, so I know we are moving in the right direction. With the most predictive features removed, it’s interesting to see that ‘belongs_to_collection’ seems to be more influencial than budget.
Regularised - Lasso
lasso = lm.Lasso(tol=5)
lasso_params = {'alpha': np.logspace(10, 100, 5),
'fit_intercept': [True, False]}
lasso_model = regularised_model_metrics(X_train, y_train, X_test, y_test, lasso, lasso_params)
Fitting 5 folds for each of 10 candidates, totalling 50 fits
[Parallel(n_jobs=-1)]: Done 42 tasks | elapsed: 2.6s
Best parameters: {'alpha': 10000000000.0, 'fit_intercept': True}
Cross-validated score on test data: $0.02
Testing RMSE: $226,516,599.51
Feature Coef Abs Coef
0 Aaron Seltzer -0.0 0.0
1402 supporting_Irene Miracle 0.0 0.0
1400 supporting_Ingrid Bergman 0.0 0.0
1399 supporting_Ichirō Nagai -0.0 0.0
1398 supporting_Ice Cube 0.0 0.0
1397 supporting_Iben Hjejle -0.0 0.0
1396 supporting_Ian McShane 0.0 0.0
1395 supporting_Ian McKellen 0.0 0.0
1394 supporting_Ian McDiarmid 0.0 0.0
1393 supporting_Ian Holm 0.0 0.0
[Parallel(n_jobs=-1)]: Done 50 out of 50 | elapsed: 3.0s finished
After a lot of tuning and increasing the alpha, lasso still didn’t perform as well as ridge. The coefficients also make less intuitive sense.
Regularised - ElasticNet
elastic = lm.ElasticNet()
elastic_params = {'alpha': np.linspace(1, 10, 10),
'l1_ratio': np.linspace(0.05, 0.95, 10),
'fit_intercept': [True, False]}
elastic_model = regularised_model_metrics(X_train, y_train, X_test, y_test, elastic,
elastic_params)
Fitting 5 folds for each of 200 candidates, totalling 1000 fits
[Parallel(n_jobs=-1)]: Done 42 tasks | elapsed: 4.7s
[Parallel(n_jobs=-1)]: Done 192 tasks | elapsed: 19.4s
[Parallel(n_jobs=-1)]: Done 442 tasks | elapsed: 34.3s
[Parallel(n_jobs=-1)]: Done 792 tasks | elapsed: 53.1s
Best parameters: {'alpha': 2.0, 'fit_intercept': True, 'l1_ratio': 0.65}
Cross-validated score on test data: $0.36
Testing RMSE: $186,283,469.11
Feature Coef Abs Coef
247 budget 1.991908e+07 1.991908e+07
249 belongs_to_collection 1.967256e+07 1.967256e+07
82 George Lucas 1.289770e+07 1.289770e+07
248 runtime 1.227358e+07 1.227358e+07
437 lead_Daniel Radcliffe 1.076488e+07 1.076488e+07
1918 supporting_Rupert Grint 1.046807e+07 1.046807e+07
251 Adventure 9.455739e+06 9.455739e+06
1395 supporting_Ian McKellen 9.207659e+06 9.207659e+06
1976 supporting_Stanley Tucci 9.097251e+06 9.097251e+06
1212 supporting_Dan Stevens 8.682729e+06 8.682729e+06
[Parallel(n_jobs=-1)]: Done 1000 out of 1000 | elapsed: 1.1min finished
This gives me very similar results to the ridge linear regression, but still doesn’t perform as well. So far, the ridge linear regression is the best performing.
Tree models
Simple decision tree
dt = get_model_metrics(X_train, y_train, X_test, y_test, tree.DecisionTreeRegressor(),
parametric=False)
dt
Training RMSE: $0.00
Testing RMSE: $189,435,992.34
Cross-validated RMSEs: [1.62986560e+08 1.50676461e+08 1.16390236e+08 1.28971798e+08
1.60756615e+08]
Mean cross-validated RMSE: $145,114,517.27
Feature Importance
247 budget 0.330288
249 belongs_to_collection 0.124512
248 runtime 0.096301
491 lead_Emma Watson 0.026973
742 lead_Mark Hamill 0.013669
37 Bryan Singer 0.012596
799 lead_Neel Sethi 0.012294
42 Christopher Nolan 0.011744
278 Thriller 0.011406
2028 supporting_Toni Collette 0.010859
DecisionTreeRegressor(criterion='mse', max_depth=None, max_features=None,
max_leaf_nodes=None, min_impurity_decrease=0.0,
min_impurity_split=None, min_samples_leaf=1,
min_samples_split=2, min_weight_fraction_leaf=0.0,
presort=False, random_state=None, splitter='best')
Simple decision trees tend to overfit, so I am not surprised by the train and test scores being what they are. However, I am surprised that the cross-validated score is quite good.
Random forest
rf = get_model_metrics(X_train, y_train, X_test, y_test, ensemble.RandomForestRegressor(),
parametric=False)
rf
Training RMSE: $51,290,496.58
Testing RMSE: $171,985,754.15
Cross-validated RMSEs: [1.30170546e+08 1.29842827e+08 9.17430304e+07 1.19111377e+08
1.27713356e+08]
Mean cross-validated RMSE: $120,597,293.25
Feature Importance
247 budget 0.324819
249 belongs_to_collection 0.119175
248 runtime 0.073327
25 Bill Condon 0.012158
226 Steven Spielberg 0.012097
742 lead_Mark Hamill 0.011958
2028 supporting_Toni Collette 0.011653
1395 supporting_Ian McKellen 0.010731
799 lead_Neel Sethi 0.010293
251 Adventure 0.009515
RandomForestRegressor(bootstrap=True, criterion='mse', max_depth=None,
max_features='auto', max_leaf_nodes=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, n_estimators=10, n_jobs=1,
oob_score=False, random_state=None, verbose=0, warm_start=False)
The best performing model so far, with feature importances that make intuitive sense.
Regularised Random forest
rrf = ensemble.RandomForestRegressor()
rrf_params = {'bootstrap': [True, False],
'max_depth': np.linspace(5, 50, 5),
'min_samples_split': np.linspace(0.1, 1, 5),
'n_estimators': [10, 15, 20]}
rrf_model = regularised_model_metrics(X_train, y_train, X_test, y_test, rrf, rrf_params,
parametric=False)
Fitting 5 folds for each of 150 candidates, totalling 750 fits
[Parallel(n_jobs=-1)]: Done 42 tasks | elapsed: 3.4s
[Parallel(n_jobs=-1)]: Done 192 tasks | elapsed: 16.4s
[Parallel(n_jobs=-1)]: Done 442 tasks | elapsed: 42.7s
[Parallel(n_jobs=-1)]: Done 750 out of 750 | elapsed: 1.7min finished
Best parameters: {'bootstrap': False, 'max_depth': 5.0, 'min_samples_split': 0.1, 'n_estimators': 10}
Cross-validated score on test data: $0.35
Testing RMSE: $188,255,673.77
Feature Importance
247 budget 0.628325
249 belongs_to_collection 0.270686
2028 supporting_Toni Collette 0.023607
248 runtime 0.015528
742 lead_Mark Hamill 0.014858
1371 supporting_Harrison Ford 0.014858
226 Steven Spielberg 0.013352
678 lead_Kathryn Beaumont 0.009393
2046 supporting_Verna Felton 0.009393
1395 supporting_Ian McKellen 0.000000
A good test score, but not quite as good as the random forest with the default parameters.
Bagged decision trees
bagdt = ensemble.BaggingRegressor()
bagdt.fit(X_train, y_train)
print('Training RMSE:', '${:,.2f}'.format(np.sqrt(metrics.mean_squared_error(y_train, bagdt.predict(X_train)))))
print('Testing RMSE:', '${:,.2f}'.format(np.sqrt(metrics.mean_squared_error(y_test, bagdt.predict(X_test)))))
cv_scores = -cross_val_score(bagdt, X_train, y_train, cv=5, scoring='neg_mean_squared_error')
print('Cross-validated RMSEs:', cv_scores)
print('Mean cross-validated RMSE:', '${:,.2f}'.format(np.mean(cv_scores)))
Training RMSE: $47,551,713.19
Testing RMSE: $167,557,918.72
Cross-validated RMSEs: [1.61524815e+16 1.63382135e+16 8.80421032e+15 1.40081532e+16
1.70218650e+16]
Mean cross-validated RMSE: $14,464,984,700,217,268.00
I am disappointed at the mean cross-validated score here - this model won’t generalise well.
Support Vector Machine
LinearSVR
lin = svm.LinearSVR()
lin_params = {
'C': np.logspace(-3, 2, 5),
'loss': ['epsilon_insensitive','squared_epsilon_insensitive'],
'fit_intercept': [True,False],
'max_iter': [1000]
}
lin_model = regularised_model_metrics(X_train, y_train, X_test, y_test, lin, lin_params)
Fitting 5 folds for each of 20 candidates, totalling 100 fits
[Parallel(n_jobs=-1)]: Done 42 tasks | elapsed: 4.6s
[Parallel(n_jobs=-1)]: Done 100 out of 100 | elapsed: 53.0s finished
Best parameters: {'C': 0.001, 'fit_intercept': True, 'loss': 'squared_epsilon_insensitive', 'max_iter': 1000}
Cross-validated score on test data: $0.07
Testing RMSE: $188,783,310.28
Feature Coef Abs Coef
249 belongs_to_collection 2.347037e+07 2.347037e+07
247 budget 2.172464e+07 2.172464e+07
82 George Lucas 1.620963e+07 1.620963e+07
248 runtime 1.470311e+07 1.470311e+07
437 lead_Daniel Radcliffe 1.180886e+07 1.180886e+07
1918 supporting_Rupert Grint 1.154390e+07 1.154390e+07
1976 supporting_Stanley Tucci 1.089841e+07 1.089841e+07
1395 supporting_Ian McKellen 1.066900e+07 1.066900e+07
251 Adventure 1.028434e+07 1.028434e+07
2028 supporting_Toni Collette 1.008356e+07 1.008356e+07
Although the test score is below baseline, the test score isn’t as good as the random forest.
RBF
rbf = svm.SVR(kernel='rbf')
rbf_params = {
'C': np.logspace(-3, 2, 5),
'gamma': np.logspace(-3, 2, 5),
'kernel': ['rbf']}
rbf = GridSearchCV(rbf, rbf_params, n_jobs=-1, cv=5, verbose=1, error_score='neg_mean_squared_error')
rbf.fit(X_train, y_train)
print('Best parameters:', rbf.best_params_)
print('Training RMSE:', '${:,.2f}'.format(abs(rbf.best_score_)))
print('Testing RMSE:', '${:,.2f}'.format(np.sqrt(metrics.mean_squared_error(y_test, rbf.best_estimator_.predict(X_test)))))
Fitting 5 folds for each of 25 candidates, totalling 125 fits
[Parallel(n_jobs=-1)]: Done 42 tasks | elapsed: 1.5min
[Parallel(n_jobs=-1)]: Done 125 out of 125 | elapsed: 4.1min finished
Best parameters: {'C': 100.0, 'gamma': 0.001, 'kernel': 'rbf'}
Training RMSE: $0.14
Testing RMSE: $240,436,736.27
This has performed worse than the LinearSVR, so I won’t be using this.
Poly
poly = svm.SVR(kernel='poly')
poly_params = {
'C': np.logspace(-3, 2, 3),
'gamma': np.logspace(-5, 2, 3),
'degree': [2]}
poly = GridSearchCV(poly, poly_params, n_jobs=-1, cv=5, verbose=1, error_score='neg_mean_squared_error')
poly.fit(X_train, y_train)
print('Best parameters:', poly.best_params_)
print('Training RMSE:', '${:,.2f}'.format(abs(poly.best_score_)))
print('Testing RMSE:', '${:,.2f}'.format(np.sqrt(metrics.mean_squared_error(y_test, poly.best_estimator_.predict(X_test)))))
Fitting 5 folds for each of 9 candidates, totalling 45 fits
[Parallel(n_jobs=-1)]: Done 45 out of 45 | elapsed: 1.5min finished
Best parameters: {'C': 0.31622776601683794, 'degree': 2, 'gamma': 100.0}
Training RMSE: $0.14
Testing RMSE: $202,171,501.80
I did play with including 3 as a degree hyperparameter, but the gridsearch took ages to run and the results didn’t improve much.
Conclusion
The best performing model is the random forest. I will pickle it, as well as exporting the scaled features as csv, and use them in my Flask app.
X_scaled = pd.concat([X_train, X_test])
y_concat = pd.concat([y_train, y_test])
X_scaled.to_csv("X_profit.csv")
rf.fit(X_scaled, y_concat)
cv_scores = -cross_val_score(rf, X_scaled, y_concat, cv=5, scoring='neg_mean_squared_error')
print('Cross-validated RMSEs:', np.sqrt(cv_scores))
print('Mean cross-validated RMSE:', '${:,.2f}'.format(np.mean(np.sqrt(cv_scores))))
Cross-validated RMSEs: [1.25429824e+08 9.88043543e+07 1.11233629e+08 1.53454944e+08
1.52458683e+08]
Mean cross-validated RMSE: $128,276,286.95
with open('model_profit.pkl', 'wb') as f:
pickle.dump(rf, f)